Neste Artigo
- Por Que a Teoria dos Conjuntos é a Base da Lógica Moderna?
- Diagramas de Venn: Sua Ferramenta de Visualização
- A Regra de Ouro para Resolução: “Comece Pelo Coração”
- Estudo de Caso: O Padrão FGV e Cebraspe
- Dicas Avançadas para Questões “Armadilha”
- O Caminho para a Aprovação
Você já se deparou com aquela questão de prova que começa descrevendo grupos de pessoas — “tantos gostam de futebol, tantos de vôlei, alguns de ambos” — e sentiu um nó na cabeça para organizar os dados? Se a resposta for sim, você não está sozinho. Em minhas análises de editais e provas recentes, de tribunais a carreiras policiais, a Teoria dos Conjuntos permanece como um dos pilares inabaláveis do Raciocínio Lógico Matemático (RLM).
Para o ciclo de concursos 2024/2025, a tendência é clara: as bancas (como FGV, Cebraspe e Vunesp) estão migrando de questões puramente mecânicas para problemas interpretativos que exigem uma visualização gráfica precisa. Não se trata apenas de decorar fórmulas, mas de entender a *arquitetura* da informação. Neste artigo, vamos desmontar esses problemas peça por peça, usando métodos que transformam a confusão em clareza visual.
1. Por Que a Teoria dos Conjuntos é a Base da Lógica Moderna?
Antes de desenharmos círculos, é crucial entender o *porquê*. A Teoria dos Conjuntos não é apenas um tópico isolado de matemática; é a linguagem fundamental da organização de dados. Em um mundo dominado por Big Data, a habilidade de categorizar informações (interseção, união, exclusão) é avaliada pelos examinadores como um reflexo da sua capacidade analítica.
Em provas de alto nível, os avaliadores buscam candidatos que consigam:
* Classificar objetos: Distinguir quem pertence a um grupo e quem está fora.
* Identificar conexões: Encontrar o ponto comum (interseção) entre categorias distintas.
* Isolar variáveis: Determinar o que é exclusivo de um subgrupo.
Aplicação no Mundo Real (e na sua Carreira)
O conhecimento que você adquire aqui vai além da prova. Profissionais de Tecnologia da Informação usam esses conceitos diariamente em Bancos de Dados (SQL)** e **Ciência de Dados. Quando um programador pede ao sistema para “buscar clientes que compraram o produto A E o produto B, mas NÃO o produto C”, ele está executando uma operação clássica de conjuntos.
2. Diagramas de Venn: Sua Ferramenta de Visualização
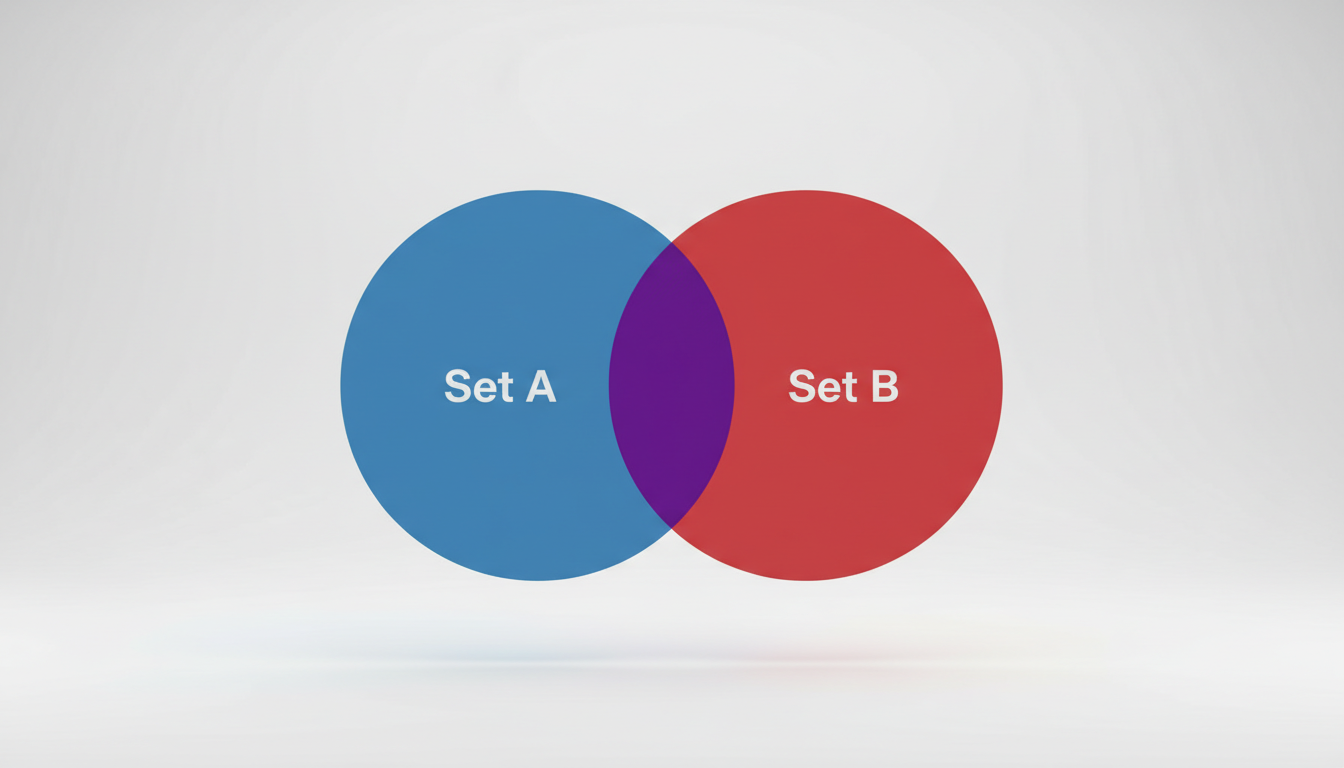
O Diagrama de Venn é a representação gráfica que salva vidas na hora da prova. Ele traduz textos complexos e ambíguos em imagens concretas.
O Básico Bem Feito: Operações Essenciais
Para dominar qualquer questão, você precisa estar íntimo de três regiões:
* Interseção (A ∩ B): É o “E”. Elementos que pertencem a AMBOS os conjuntos simultaneamente. É o coração do diagrama.
* União (A ∪ B): É o “OU”. Tudo que está em A, tudo que está em B, ou em ambos. *Atenção: no Raciocínio Lógico, o “ou” é inclusivo.*
* Diferença (A – B): O famoso “Apenas A”. São os elementos que estão em A, mas estritamente fora de B.
3. A Regra de Ouro para Resolução: “Comece Pelo Coração”
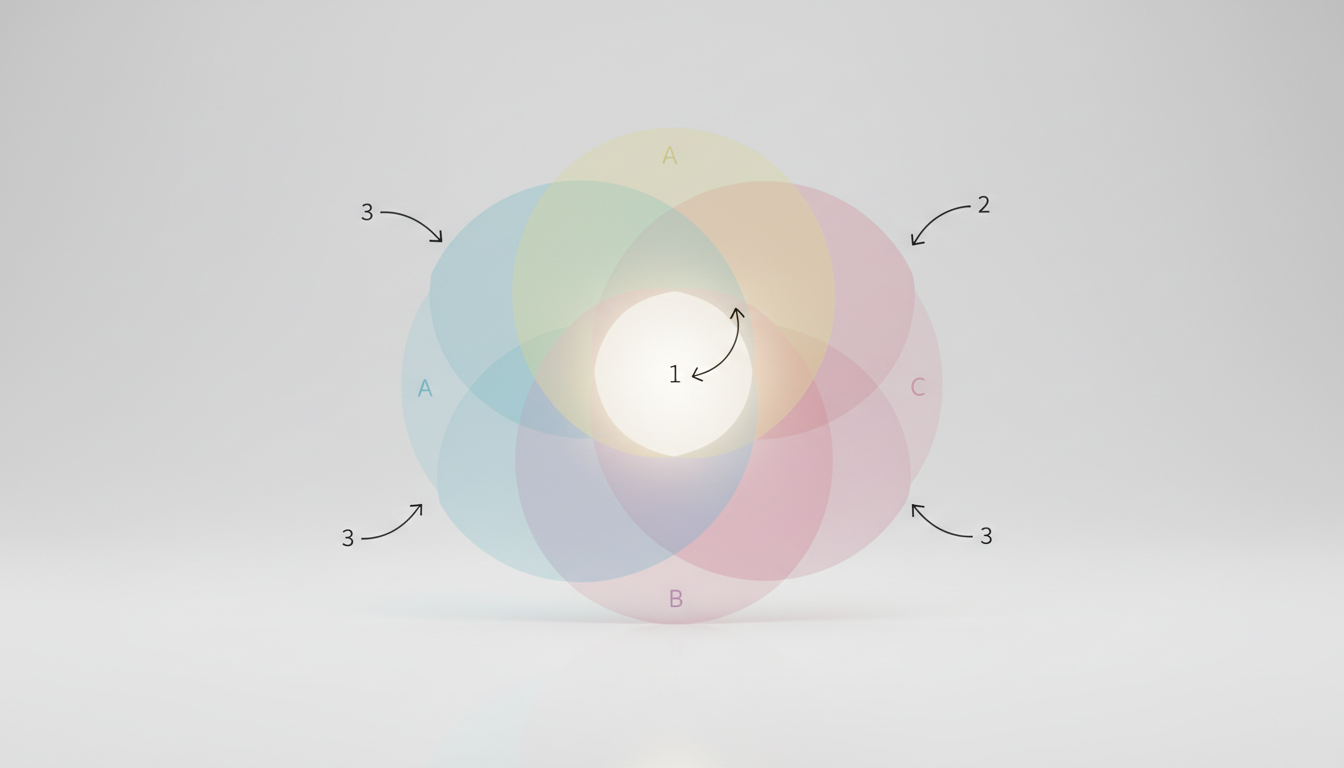
Aqui está o segredo que diferencia os candidatos aprovados da maioria: sempre comece preenchendo a interseção mais central.
Se o problema envolve três conjuntos (A, B e C), a tentação é começar pelos dados unitários (“20 pessoas gostam de A”). Não faça isso. Se você começar pelas bordas, terá que corrigir os números depois, o que leva ao erro.
Metodologia Passo a Passo (Protocolo 2025):
1. Identifique a Interseção Central: Procure no texto o número de elementos que pertencem a *todos* os conjuntos (ex: “5 pessoas gostam das três marcas”). Coloque esse número bem no meio.
2. Expanda para as Interseções Duplas: Subtraia o valor central. Se a questão diz “10 gostam de A e B” e você já colocou 5 no centro (A, B e C), então na região exclusiva de “A e B” você colocará apenas 5 (10 – 5).
3. Preencha os Valores Individuais: Subtraia todas as interseções que já estão dentro do círculo daquele conjunto.
4. Não Esqueça o “Nenhum”: O valor de quem não pertence a nenhum conjunto fica dentro do retângulo universal, mas fora dos círculos.
4. Estudo de Caso: O Padrão FGV e Cebraspe
Vamos analisar como isso aparece na prática. Imagine o seguinte cenário típico de uma prova de Tribunal ou Polícia Civil:
> *”Em uma delegacia, de 100 inquéritos, 40 envolvem furto, 30 envolvem estelionato e 10 envolvem ambos. Quantos inquéritos não envolvem nem furto nem estelionato?”*
Resolução Estratégica:
1. Desenhe: Dois círculos entrelaçados (Furto e Estelionato).
2. Interseção:** Comece pelo “ambos”. Coloque **10 no meio.
3. Furto (Exclusivo):** O total é 40. Já temos 10 no meio. Então, apenas furto = 40 – 10 = **30.
4. Estelionato (Exclusivo):** O total é 30. Já temos 10 no meio. Apenas estelionato = 30 – 10 = **20.
5. Soma das Partes:** 30 (só furto) + 10 (ambos) + 20 (só estelionato) = **60 inquéritos catalogados nos conjuntos.
6. O Resultado:** Se o total é 100, então 100 – 60 = **40 inquéritos não envolvem nenhum dos dois.
Perceba que sem subtrair a interseção, você somaria 40 + 30 = 70, errando a conta final. A precisão está na subtração.
5. Dicas Avançadas para Questões “Armadilha”
* “Pelo menos um”:** Essa expressão é código para **União. Se a questão pede a probabilidade de escolher alguém que goste de “pelo menos um”, ela quer (A ∪ B ∪ C).
* Subconjuntos Ocultos: Às vezes, o texto diz “Todo A é B”. Isso significa que o círculo A deve ser desenhado *dentro* do círculo B. Não há interseção parcial, há inclusão total.
* O Valor Desconhecido (x):** Se a banca não der a interseção central, chame-a de **x e monte uma equação linear simples. É a técnica favorita da Vunesp.
O Caminho para a Aprovação
A Teoria dos Conjuntos é um daqueles tópicos gratos: uma vez que você entende o mecanismo visual, é difícil “desaprender”. Não exige memorização de leis ou prazos, apenas lógica pura. Para 2025, minha recomendação é praticar exaustivamente o preenchimento de diagramas de três conjuntos, pois é onde a maioria dos candidatos se perde na contabilidade dos elementos.
Ao dominar essa ferramenta, você ganha não apenas pontos em Raciocínio Lógico, mas desenvolve uma mente mais analítica e preparada para tomar decisões baseadas em dados — uma competência essencial para o servidor público moderno.
Autor: Carlos Mendes é especialista em Raciocínio Lógico e Matemática para concursos públicos com mais de 10 anos de experiência em preparação de alto rendimento. Engenheiro por formação e entusiasta da Ciência de Dados, Carlos aplica metodologias analíticas para simplificar a aprendizagem de exatas, ajudando milhares de alunos a perderem o medo dos números e conquistarem a aprovação.