Neste Artigo
- A Matemática é o “Calcanhar de Aquiles” dos Concursos?
- 1. O Fundamento Lógico: Grandeza e Proporcionalidade
- 2. Regra de Três Simples: O Passo a Passo Seguro
- 3. Regra de Três Composta: O Método “Processo vs. Produto”
- 4. O Novo Perfil das Questões em 2025: Letramento Matemático
- 5. Erros Fatais para Evitar
- Preparação Estratégica
A Matemática é o “Calcanhar de Aquiles” dos Concursos? Não Precisa Ser.
Se você sente um frio na espinha ao ler um enunciado de matemática em uma prova, saiba que não está sozinho. Dados recentes de 2024 e projeções para 2025 indicam que a Matemática continua sendo a disciplina de maior dificuldade para candidatos do ENEM e de Concursos Públicos, com cerca de 52% dos estudantes apontando-a como o principal obstáculo para a aprovação.
No entanto, existe uma ferramenta poderosa, quase uma “chave mestra”, capaz de resolver cerca de 40% das questões de raciocínio lógico e matemática básica: a Regra de Três. Seja para calcular dosagens de medicamentos em provas de enfermagem, ajustar receitas industriais ou resolver problemas de logística no Concurso Nacional Unificado (CNU), dominar este conceito não é apenas útil—é obrigatório.
Neste artigo premium, vamos além da simples “multiplicação em cruz”. Você aprenderá a interpretar enunciados complexos (uma tendência forte para as bancas de 2025), diferenciar grandezas inversas sem cair em pegadinhas e dominar o método do “Processo vs. Produto” para Regra de Três Composta, eliminando a confusão das setinhas para sempre.
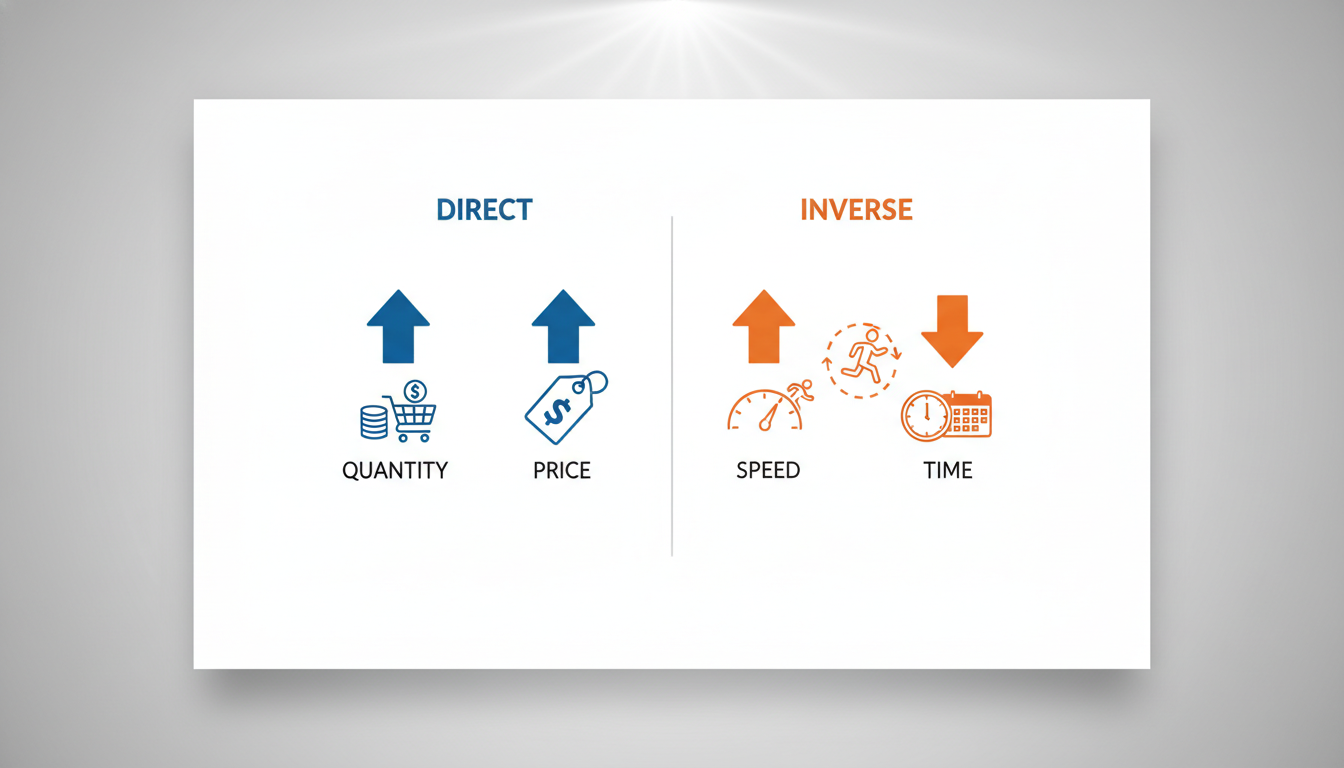
1. O Fundamento Lógico: Grandeza e Proporcionalidade
Antes de decorarmos qualquer método de resolução, precisamos entender o “código fonte” da Regra de Três: a proporcionalidade. A maioria dos erros ocorre não no cálculo, mas na identificação da relação entre as grandezas.
Uma grandeza é tudo aquilo que pode ser medido ou contado: tempo, velocidade, quantidade de pessoas, produção, dinheiro, etc. O segredo está em como duas grandezas “conversam” entre si.
Diretamente Proporcional (A Regra do “Mais é Mais”)
Duas grandezas são diretamente proporcionais quando, ao aumentarmos uma, a outra também aumenta na mesma proporção. É intuitivo:
- Se compro mais canetas, gasto mais dinheiro.
- Se um carro percorre uma distância em velocidade constante, quanto mais tempo ele viaja, maior a distância percorrida.
Inversamente Proporcional (A Armadilha Comum)
Aqui reside a maior fonte de erros em concursos. Grandezas são inversamente proporcionais quando o aumento de uma causa a diminuição da outra.
- Velocidade x Tempo: Se aumento a velocidade do carro, gasto menos tempo para chegar.
- Operários x Prazo: Se contrato mais pedreiros, o muro fica pronto em menos dias.
Atenção: Em 2025, as bancas (como Cebraspe e FGV) têm apostado em enunciados longos que escondem essa relação inversa. O aluno desatento aplica a regra direta (multiplica cruzado) e encontra uma resposta que, infelizmente, estará lá nas alternativas (o famoso “distrator”).
2. Regra de Três Simples: O Passo a Passo Seguro
A Regra de Três Simples relaciona apenas duas grandezas. O método clássico funciona perfeitamente, desde que você siga um protocolo rígido de organização.
Cenário A: Grandezas Diretamente Proporcionais
Exemplo: Se 5 kg de café custam R$ 120,00, quanto custarão 12 kg do mesmo café?
- Montagem da Tabela: Coloque grandezas iguais na mesma coluna.
Kg | Preço (R$)5 | 12012 | x - Análise: Se aumento a quantidade (de 5 para 12), o preço aumenta? Sim. (Direta).
- Cálculo: Multiplique cruzado (em X).
5 * x = 12 * 1205x = 1440
x = 1440 / 5
x = R$ 288,00
Cenário B: Grandezas Inversamente Proporcionais
Exemplo: Uma equipe de 6 pintores termina um serviço em 10 dias. Se a equipe fosse reforçada para 15 pintores (com mesmo ritmo), em quantos dias terminariam?
- Montagem da Tabela:
Pintores | Dias6 | 1015 | x - Análise Crucial: Se aumento o número de pintores, o tempo aumenta ou diminui? Diminui. Logo, é INVERSA.
- O Ajuste: Antes de multiplicar, você deve inverter uma das colunas ou multiplicar “em linha” (reto), nunca cruzado.
Método Reto (para inversas):15 * x = 6 * 10
15x = 60
x = 60 / 15
x = 4 dias
Perceba: Se você tivesse multiplicado cruzado (15*10 = 150 / 6 = 25 dias), a resposta não faria sentido lógico (mais gente demorando mais tempo?). Sempre faça o “teste de realidade” ao final.
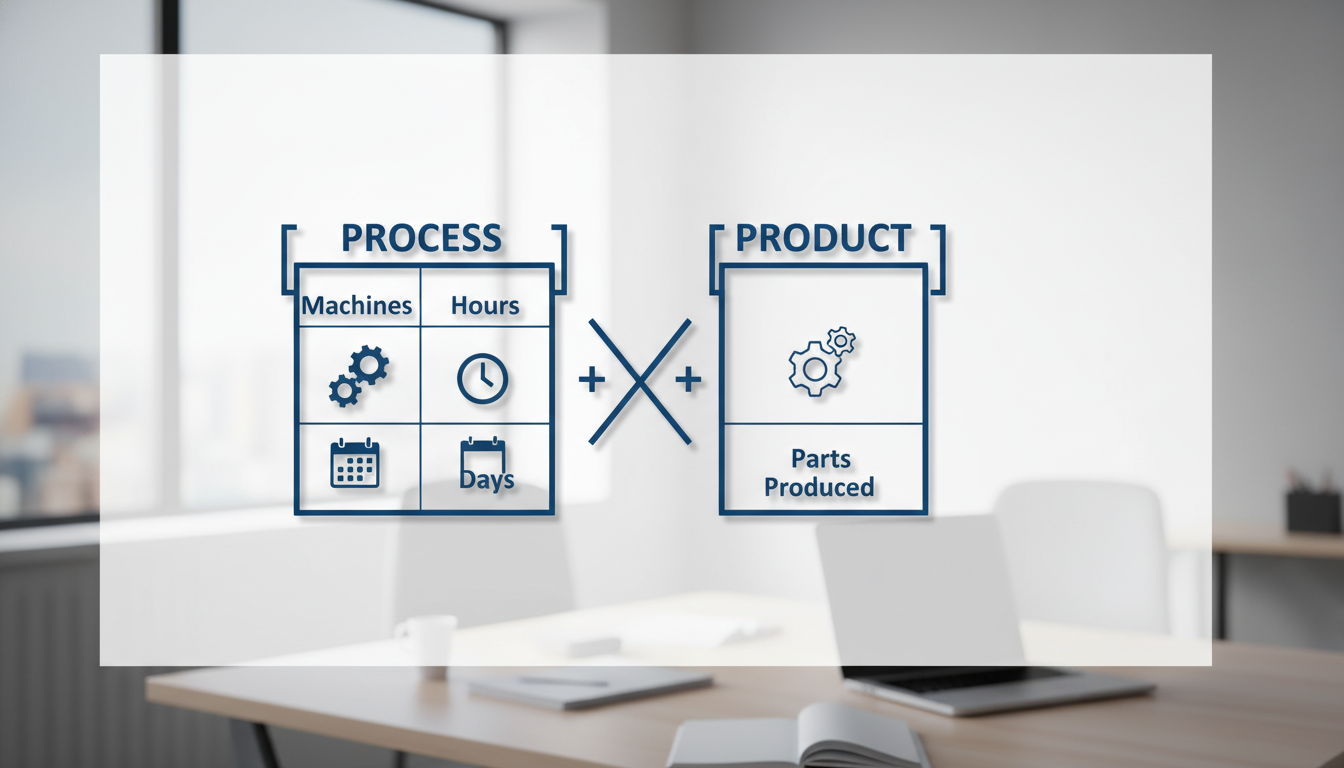
3. Regra de Três Composta: O Método “Processo vs. Produto” (Sem Setinhas)
A Regra de Três Composta envolve mais de duas grandezas (ex: operários, horas por dia, dias, metros de muro). O método tradicional ensinado nas escolas envolve desenhar setinhas para cima e para baixo, o que gera confusão visual e erros frequentes sob a pressão do tempo de prova.
Para o nível de exigência atual, recomendamos o Método do Processo vs. Produto. É uma técnica mecânica que elimina a dúvida sobre quem multiplica quem.
Como funciona o Método:
A lógica é separar as grandezas em dois grupos:
- PROCESSO: Tudo que trabalha ou influencia o trabalho (Pessoas, Máquinas, Horas/dia, Dias, Eficiência).
- PRODUTO: O resultado final do trabalho (O muro construído, as peças fabricadas, a distância percorrida, o relatório digitado).
Exemplo Prático e Complexo
Problema: 4 máquinas, operando 6 horas por dia durante 5 dias, produzem 2.000 peças. Quantas peças serão produzidas por 3 máquinas, operando 8 horas por dia durante 10 dias?
Passo 1: Identificar as Colunas
- Processo (Quem faz): Máquinas, Horas/dia, Dias.
- Produto (O feito): Peças.
Passo 2: Montar o Esquema
Coloque os valores lado a lado, separando Processo de Produto.
MÁQUINASHORAS/DIADIAS|PEÇAS (Produto)465|2.0003810|x
Passo 3: A Multiplicação em “X” Gigante
A regra é simples: Multiplique todos os valores da linha de cima do Processo pelo valor da linha de baixo do Produto. E vice-versa. As linhas se cruzam apenas na barreira entre Processo e Produto.
- Linha 1 (Processo) descendo para Produto: 4 * 6 * 5 * x
- Linha 2 (Processo) subindo para Produto: 3 * 8 * 10 * 2.000
Passo 4: Igualar e Resolver
(4 * 6 * 5) * x = (3 * 8 * 10) * 2.000
120 * x = 240 * 2.000
120x = 480.000
x = 480.000 / 120
x = 4.000 peças
Por que este método é superior? Porque você não precisa analisar se “horas” é inverso a “dias” ou direto a “peças”. A estrutura matemática do método já compensa automaticamente as proporcionalidades inversas. Em uma prova cansativa, isso vale ouro.
4. O Novo Perfil das Questões em 2025: Letramento Matemático
Ao analisar as tendências educacionais e editais recentes (como o da Banca Cesgranrio para o CNU ou o INEP para o ENEM), percebe-se uma mudança. As questões secas do tipo “Calcule X” estão dando lugar a problemas contextualizados.
O que isso significa para você? Que a dificuldade não estará na conta, mas na montagem. Você encontrará textos sobre sustentabilidade, economia de energia ou demografia. O desafio será filtrar, dentro de 10 linhas de texto, quais são as grandezas Relevantes (Processo) e qual é o objetivo (Produto).
Dica de Ouro: Sempre pergunte ao texto: “O que está sendo produzido ou realizado?”. Se o problema fala de pintores pintando uma parede, o produto é a parede. Se fala de impressoras imprimindo folhas, o produto são as folhas. Se fala de comida consumida por náufragos, o produto é a comida (neste caso, o consumo). Identificou o produto? O resto é processo.
5. Erros Fatais para Evitar
- Conversão de Unidades: Misturar horas com minutos. Se o enunciado der “1h 30min”, converta tudo para minutos (90 min) antes de colocar na regra de três. Nunca use “1,30” para representar uma hora e meia (o correto decimal seria 1,5).
- Achar que tudo é Regra de Três: Progressões Aritméticas (PA) e Geométricas (PG) às vezes se disfarçam de problemas proporcionais, mas não são. Se o crescimento for exponencial (ex: bactérias que duplicam a cada hora), a regra de três simples falhará. Use-a apenas para relações lineares.
Preparação Estratégica
A Regra de Três é a base da pirâmide do conhecimento matemático para concursos. Dominá-la não apenas garante os pontos dessas questões específicas, mas também destrava o entendimento de Porcentagem, Matemática Financeira (Juros) e Geometria Plana (Semelhança de Triângulos).
Para consolidar esse conhecimento, a prática deve ser constante. Comece identificando em seu dia a dia situações de proporcionalidade. Quanto mais natural esse raciocínio se tornar, mais rápida será sua aprovação.
Autor: Prof. Carlos Mendes é matemático e especialista em preparação para concursos públicos há mais de 15 anos. Com foco em Raciocínio Lógico-Matemático, desenvolveu metodologias de aprendizado acelerado que ajudaram centenas de alunos a superarem o bloqueio com as exatas. Acompanha anualmente as tendências das bancas como FGV, Cebraspe e Cesgranrio.