Neste Artigo
- O Erro Número 1: A Tentação de Somar Porcentagens
- Método Prático 1: A Regra dos “100 Reais”
- Método Profissional: Fatores de Multiplicação (VM)
- Aplicação em Cenários Reais de 2025
- Dicas de Ouro para o Dia da Prova
A matemática financeira e o raciocínio lógico continuam sendo o “calcanhar de Aquiles” para milhares de candidatos em 2025. Se você está se preparando para o Concurso Nacional Unificado (CNU), carreiras bancárias ou tribunais, provavelmente já se deparou com a clássica pegadinha: “Se um produto aumenta 10% e depois desconta 10%, ele volta ao preço original?”
A resposta intuitiva é “sim”, mas a resposta matemática — e a única que garante sua aprovação — é um sonoro não.
Neste artigo, vamos desmistificar o cálculo de porcentagens sucessivas. Diferente do que muitos pensam, não é necessário decorar fórmulas complexas. O segredo está em entender a lógica dos *fatores de multiplicação*. Dominar essa técnica não apenas garante pontos preciosos em provas como a da Cesgranrio, Cebraspe ou FGV, mas também protege seu bolso na vida real contra promoções enganosas.
O Erro Número 1: A Tentação de Somar Porcentagens
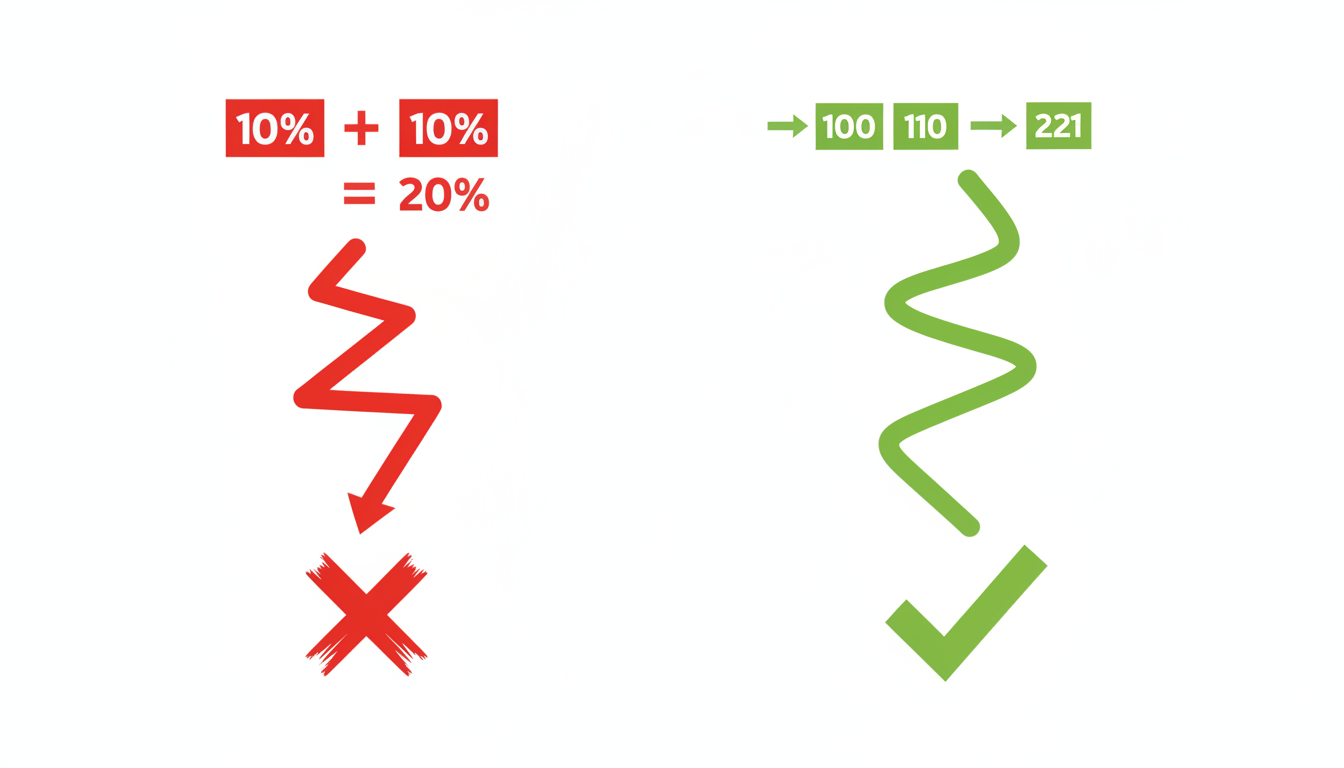
O erro mais comum, que elimina candidatos bem preparados em outras matérias, é a soma algébrica direta das taxas.
Imagine um cenário de inflação onde um item sobe 20% em um mês e 30% no mês seguinte. O raciocínio rápido sugere um aumento total de 50%. No entanto, o segundo aumento incide sobre um valor *já alterado*, criando um efeito de “juros sobre juros”.
Em 2025, as bancas examinadoras têm apostado em enunciados que exploram exatamente essa falha cognitiva. Elas sabem que, sob pressão, o cérebro busca o caminho mais curto (a soma).
Método Prático 1: A Regra dos “100 Reais”
Para quem tem dificuldade com abstração ou variáveis $x$, o método mais seguro e didático é atribuir um valor inicial fictício de R$ 100,00. Como a porcentagem é uma razão centesimal, o número 100 facilita imensamente as contas.
Exemplo Prático: Aumento e Desconto
Questão: Uma loja aumentou o preço de uma TV em 20%. Meses depois, ofereceu um desconto de 20% sobre o novo preço. O valor final é igual ao inicial?
Resolução Passo a Passo:
1. Valor Inicial: Suponha R$ 100,00.
2. Primeiro Movimento (Aumento de 20%):
* 20% de 100 = R$ 20,00.
* Novo preço = R$ 120,00.
3. Segundo Movimento (Desconto de 20%):
* Atenção: O desconto é sobre R$ 120,00, não sobre os 100 originais.
* 20% de 120 = R$ 24,00 (basta multiplicar 12 x 2).
* Preço Final = 120 – 24 = R$ 96,00.
Resultado:** O preço final é R$ 96,00. Comparado aos R$ 100,00 iniciais, houve uma **redução real de 4%, e não um retorno ao valor original.
Método Profissional: Fatores de Multiplicação (VM)
Para ganhar velocidade em provas de alto nível, como Auditor Fiscal ou Analista do Banco Central, você deve abandonar a regra de três e usar os Fatores de Multiplicação.
O conceito é simples: para aumentar um valor, multiplicamos por $(1 + taxa)$. Para descontar, multiplicamos por $(1 – taxa)$.
* Aumento de 10%:** Multiplique por **1,10.
* Aumento de 25%:** Multiplique por **1,25.
* Desconto de 10%:** Multiplique por **0,90.
* Desconto de 5%:** Multiplique por **0,95.
Como Calcular Variações Sucessivas Rapidamente
Se você tiver três aumentos sucessivos de 10%, 20% e 30%, a conta acumulada é apenas o produto dos fatores:
$$Fator Total = 1,10 \times 1,20 \times 1,30$$
Ao resolver $1,1 \times 1,2 = 1,32$. Depois, $1,32 \times 1,3 = 1,716$.
Isso significa que o valor final é 1,716 vezes o inicial, ou seja, um aumento total de 71,6%.

Aplicação em Cenários Reais de 2025
As questões atuais não pedem apenas o cálculo mecânico; elas contextualizam com economia real.
Cenário: Recuperação Salarial
Um servidor teve seu salário reduzido em 10% durante uma crise. Para voltar exatamente ao valor original, de quanto deve ser o aumento percentual subsequente?
Muita gente responde “10%” e erra. Vamos usar a lógica:
1. Salário inicial: 100.
2. Redução de 10%: Vai para 90.
3. Objetivo: Voltar para 100.
4. Diferença necessária: 10 unidades.
A pergunta agora é: “10 unidades representam quantos por cento de 90?”
$$ \frac{10}{90} \approx 0,1111… $$
Ou seja, é necessário um aumento de aproximadamente 11,11% para recuperar a perda de 10%.
Dicas de Ouro para o Dia da Prova
1. Simplifique as Frações: Se o fator for 1,25, lembre-se que isso é $5/4$. Multiplicar frações as vezes é mais rápido que multiplicar decimais.
2. Ordem dos Fatores: Na multiplicação, a ordem não altera o produto. Um aumento de 20% seguido de um desconto de 10% dá o mesmo resultado que um desconto de 10% seguido de um aumento de 20%.
* $1,20 \times 0,90 = 1,08$
* $0,90 \times 1,20 = 1,08$
3. Verificação de Realidade: Se houver aumentos sucessivos, o resultado final deve ser *maior* que a soma simples. Se houver descontos sucessivos, o desconto total será *menor* que a soma simples dos descontos.
Preparação Contínua
Entender a lógica das porcentagens sucessivas é um divisor de águas. Não se trata apenas de passar em uma prova, mas de adquirir uma competência analítica fundamental para a leitura de dados econômicos e financeiros.
Pratique com questões de provas anteriores (2023-2024) das bancas que você pretende prestar. A matemática não muda, mas a forma como as bancas contam a “história” do problema se torna cada vez mais sofisticada. Mantenha a calma, use o método dos 100 reais se travar, e confie no seu raciocínio.
Autor: Carlos Mendes é especialista em Raciocínio Lógico-Matemático e analista de dados com mais de 10 anos de experiência em preparação para concursos públicos de alto nível. Focado em didática simplificada, ajuda candidatos a superarem o bloqueio com as exatas através de métodos lógicos e diretos.